お店のコメント(スペック情報を含む場合もあり)
内容説明
The theory of Kac lagebras and their duality, elaborated independently in the seventies by Kac and Vainermann and by the authors of this book, has nowreached a state of maturity which justifies the publication of a comprehensive and authoritative account in bookform. Further, the topic of ?quantum groups? has recently become very fashionable and attracted the attention of more and more mathematicians and theoretical physicists. However a good characterization of quantum groups among Hopf algebras in analogy to the characterization of Lie groups among locally compact groups is still missing. It is thus very valuable to develop the generaltheory as does this book, with emphasis on the analytical aspects of the subject instead of the purely algebraic ones. While in the Pontrjagin duality theory of locally compact abelian groups a perfect symmetry exists between a group and its dual, this is no longer true in the various duality theorems of Tannaka, Krein, Stinespring and others dealing with non-abelian locally compact groups. Kac (1961) and Takesaki (1972) formulated the objective of finding a good category of Hopf algebras, containing the category of locally compact groups and fulfilling a perfect duality. The category of Kac algebras developed in this book fully answers the original duality problem, while not yet sufficiently non-unimodular to include quantum groups. This self-contained account of thetheory will be of interest to all researchers working in quantum groups, particularly those interested in the approach by Lie groups and Lie algebras or by non-commutative geometry, and more generally also to those working in C* algebras or theoretical physics.
Book Description
The theory of Kac lagebras and their duality, elaborated independently in the seventies by Kac and Vainermann and by the authors of this book, has now reached a state of maturity which justifies the publication of a comprehensive and authoritative account in bookform. Further, the topic of ?quantum groups? has recently become very fashionable and attracted the attention of more and more mathematicians and theoretical physicists. However a good characterization of quantum groups among Hopf algebras in analogy to the characterization of Lie groups among locally compact groups is still missing. It is thus very valuable to develop the general theory as does this book, with emphasis on the analytical aspects of the subject instead of the purely algebraic ones. While in the Pontrjagin duality theory of locally compact abelian groups a perfect symmetry exists between a group and its dual, this is no longer true in the various duality theorems of Tannaka, Krein, Stinespring and others dealing with non-abelian locally compact groups. Kac (1961) and Takesaki (1972) formulated the objective of finding a good category of Hopf algebras, containing the category of locally compact groups and fulfilling a perfect duality. The category of Kac algebras developed in this book fully answers the original duality problem, while not yet sufficiently non-unimodular to include quantum groups. This self-contained account of the theory will be of interest to all researchers working in quantum groups, particularly those interested in the approach by Lie groups and Lie algebras or by non-commutative geometry, and more generally also to those working in C* algebras or theoretical physics.
--このテキストは、絶版本またはこのタイトルには設定されていない版型に関連付けられています。
商品ジャンル
商品名
最終調査日時
2013/07/14 (Sun) 23:34:26
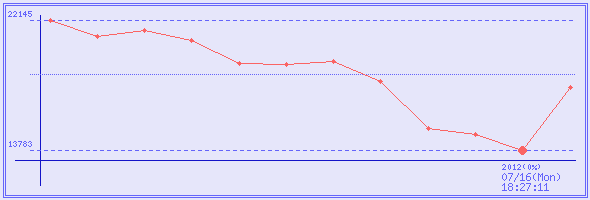
価格の変動(直近3回 : ¥0は未調査回)
取得日時
販売価格
ポイント
実質価格
在庫状態
2013/07/14 (Sun) 23:34:26
¥17,821
0 %
¥17,821
2012/07/16 (Mon) 18:27:11
¥13,783
0 %
¥13,783
2012/01/01 (Sun) 13:20:28
¥14,807
0 %
¥14,807
サイト内キーワード検索
商品名の検索は通常の商品検索ボックスで。
コメントやスペックなどから検索したい場合はこちらから。
コメントやスペックなどから検索したい場合はこちらから。
広告


![【クリックでお店のこの商品のページへ】Kac Algebras and Duality of Locally Compact Groups [ハードカバー]](http://ec2.images-amazon.com/images/I/418JG2NA17L._BO2,204,203,200_PIsitb-sticker-arrow-click,TopRight,35,-76_AA240_SH20_OU09_.jpg)


